Discovery
Go 语言中的零拷贝优化
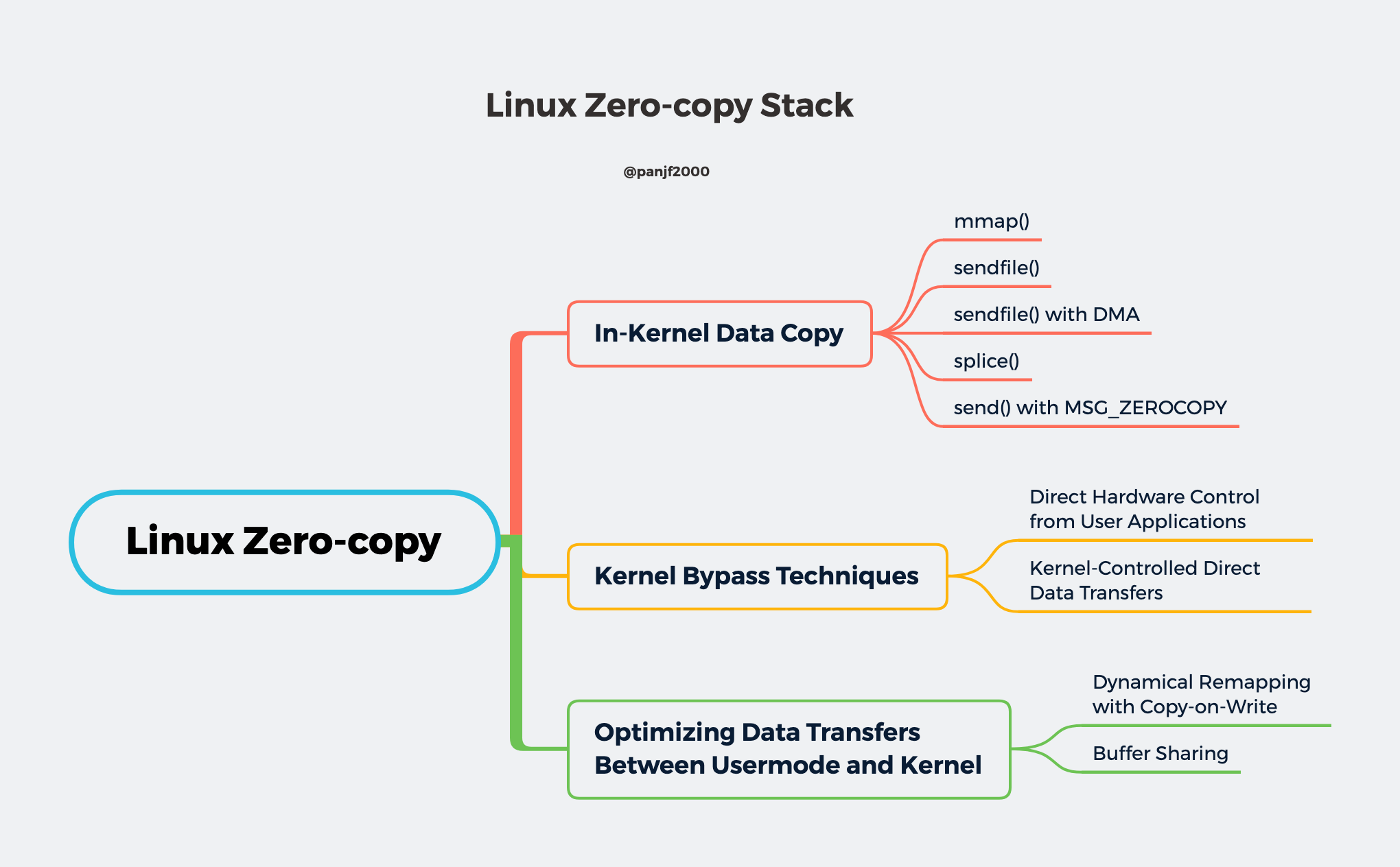
相信那些曾经使用 Go 写过 proxy server 的同学应该对 io.Copy()/io.CopyN()/io.CopyBuffer()/io.ReaderFrom 等接口和方法不陌生,它们是使用 Go 操作各类 I/O 进行数据传输经常需要使用到的 API,其中基于 TCP 协议的 socket 在使用上述接口和方法进行数据传输时利用到了 Linux 的零拷贝技术 sendfile 和 splice。 我前段时间为 Go 语言内部的 Linux splice 零拷贝技术做了一点优化:为 splice 实现了一个 pipe pool,复用管道,减少频繁创建和销毁 pipe buffers 所带来的系统开销,理论上来说能够大幅提升 Go 的 io 标准库中基于 splice 零拷贝实现的 API 的性能。因此,我想从这个优化工作出发,分享一些我个人对多线程编程中的一些不成熟的优化思路。
Linux I/O 原理和 Zero-copy 技术全面揭秘
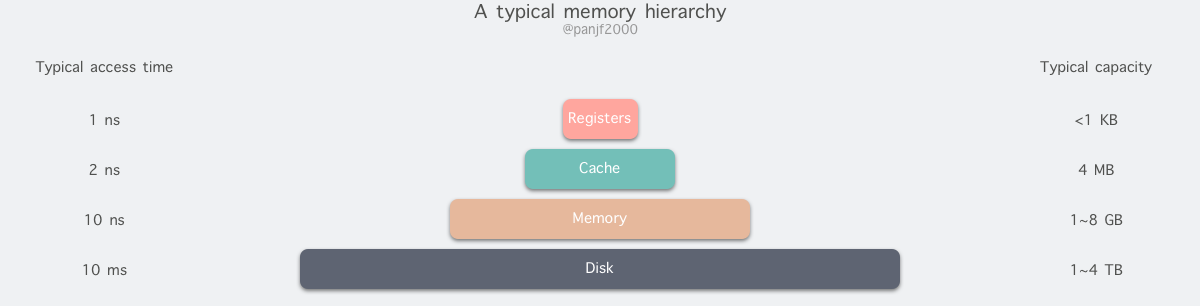
如今的网络应用早已从 CPU 密集型转向了 I/O 密集型,网络服务器大多是基于 C-S 模型,也即 客户端 - 服务端 模型,客户端需要和服务端进行大量的网络通信,这也决定了现代网络应用的性能瓶颈:I/O。 传统的 Linux 操作系统的标准 I/O 接口是基于数据拷贝操作的,即 I/O 操作会导致数据在操作系统内核地址空间的缓冲区和应用程序地址空间定义的缓冲区之间进行传输。设置缓冲区最大的好处是可以减少磁盘 I/O 的操作,如果所请求的数据已经存放在操作系统的高速缓冲存储器中,那么就不需要再进行实际的物理磁盘 I/O 操作;然而传统的 Linux I/O 在数据传输过程中的数据拷贝操作深度依赖 CPU,也就是说 I/O 过程需要 CPU 去执行数据拷贝的操作,因此导致了极大的系统开销,限制了操作系统有效进行数据传输操作的能力。 I/O 是决定网络服务器性能瓶颈的关键,而传统的 Linux I/O 机制又会导致大量的数据拷贝操作,损耗性能,所以我们亟需一种新的技术来解决数据大量拷贝的问题,这个答案就是零拷贝(Zero-copy)。